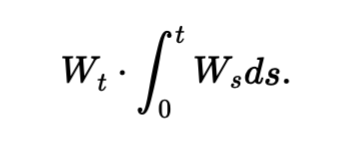Stochastic Models and Processes · 17. juin 2024
Comprenez l'interaction complexe entre le processus de Wiener \( W_t \) et son intégrale ∫ de 0 à t \( W_s \) ds. Ce produit stochastique nécessite des outils comme le lemme d'Itô pour analyser sa nature non linéaire. La covariation quadratique éclaire le comportement conjoint de ces processus, essentiel pour le pricing d'options exotiques, comme les options asiatiques.
Processus et Modèles Stochastiques · 29. juillet 2023
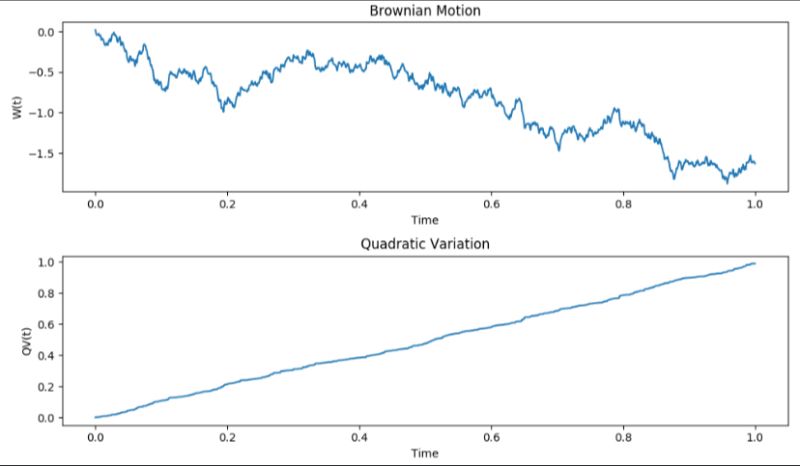
La variation quadratique en finance mesure la volatilité des mouvements de prix d’actifs, essentielle pour comprendre l'irrégularité des marchés et évaluer les risques dans le trading et la modélisation des options.
Processus et Modèles Stochastiques · 04. février 2023
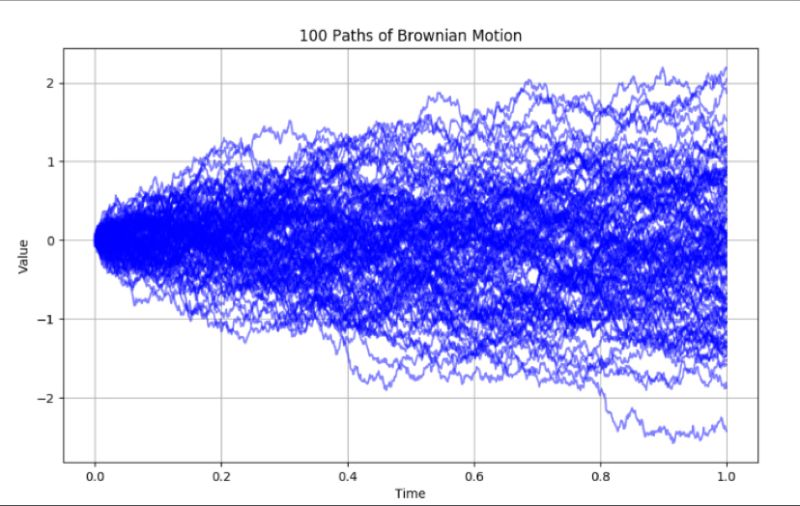
Le mouvement brownien modélise des trajectoires aléatoires en finance, avec une variance proportionnelle au temps. Son utilisation dans le modèle Black-Scholes permet de comprendre l’évolution des prix d’options et les risques associés sur des horizons temporels variables.