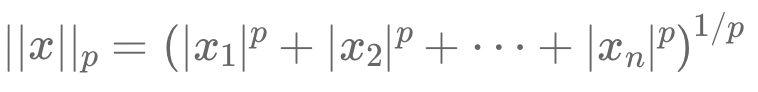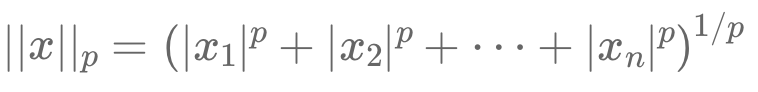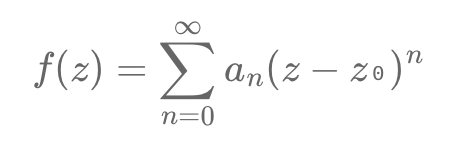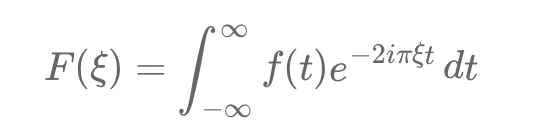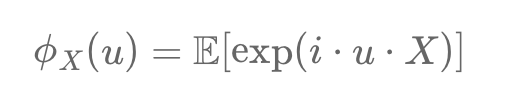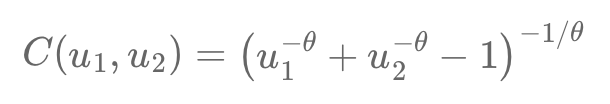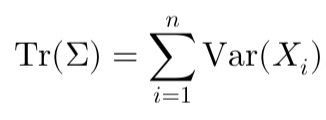Mathematical Principles and Quantitative Finance · 21. décembre 2024
The Cauchy problem solves differential equations with specific initial conditions, widely applied in modeling dynamic systems in physics, engineering, and finance. It addresses both ordinary differential equations (ODEs) for deterministic systems and stochastic differential equations (SDEs) for random processes, such as asset price modeling.
Mathematical Principles and Quantitative Finance · 19. décembre 2024
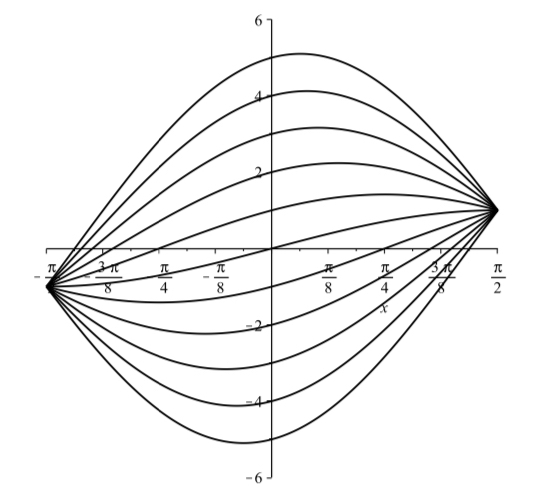
This article explains the concept of mathematical norms and their critical role in quantitative finance. Norms measure the size or length of vectors within a vector space, making them essential tools for analyzing financial data. The L1 norm (sum of absolute deviations) is highlighted for its ability to promote sparsity in portfolio optimization, while the L3 norm is presented as a tool for emphasizing extreme values.
Principes mathématiques et applications en finance · 19. décembre 2024
Cet article explique le concept des normes mathématiques et leur rôle crucial en finance quantitative. Les normes mesurent la taille ou la longueur des vecteurs dans un espace vectoriel, ce qui en fait des outils essentiels pour analyser les données financières.
Mathematical Principles and Quantitative Finance · 01. octobre 2024
In quantitative finance, pricing conditional derivatives, like options, requires ensuring that price functions converge, meaning they stabilize as calculations are refined. Compact and closed sets in complex space help ensure this stability by keeping sequences bounded and finite. Analytic functions, which smoothly represent derivative prices, rely on this convergence for accuracy.
The Cauchy integral formula enables finding a function's value by integrating along a boundary contour.
01. octobre 2024
Les nombres premiers sont les blocs de construction de tous les nombres entiers – des entiers supérieurs à 1 qui n'ont pas de diviseurs autres que 1 et eux-mêmes, comme 2, 3, 5 et 7 (2 étant le seul nombre premier pair). Euclide, le mathématicien grec ancien, a démontré qu'il existe une infinité de nombres premiers.
Pricing and Valuing Financial Instruments · 30. septembre 2024
Option pricing, a key financial market challenge, relies on the Fourier transform to address complexities in valuation. An option grants the right to buy or sell an asset at a strike price, K, by expiration, T. The current price depends on the expected payoff, e.g., for a European call: max(S_T - K, 0). This is challenging as future asset prices follow complex stochastic processes.
The Fourier transform simplifies this by converting payoff calculations from time to frequency domain.
Mathematical Principles and Quantitative Finance · 30. septembre 2024
The characteristic function of a real random variable X encodes its entire probability distribution and uniquely determines it. It is defined as:
φ_X(u) = E[exp(i * u * X)],
where E[.] is the expectation, u is a real "frequency" parameter, and i is the imaginary unit (i² = -1). The function transforms the distribution of X into the frequency domain using Fourier analysis.
For a random variable with density f_X(x):
φ_X(u) = ∫[exp(i * u * x) * f_X(x) dx] (Fourier transform).
Mathematical Principles and Quantitative Finance · 30. septembre 2024
Copulas help model dependencies between variables separately from their behaviors, crucial for finance's complex relationships. For example, Alice and Bob’s race times show dependency when transformed into uniform variables using cumulative distribution functions (CDFs). The Clayton copula captures asymmetric dependence, especially in lower tail risks, using the formula:
C(u1, u2) = (u1^(-θ) + u2^(-θ) - 1)^(-1/θ).
Mathematical Principles and Quantitative Finance · 29. septembre 2024
Topology, from Greek "topos" (place) and "logos" (study), explores connections within spaces, focusing on structure over distance. In quantitative finance, topology is crucial for derivatives pricing, ensuring stable models and smooth price changes. It supports the convergence of models like binomial trees and Monte Carlo simulations, enhancing accuracy.
A key principle in finance is the absence of arbitrage – no risk-free profit.
Mathematical Principles and Quantitative Finance · 29. septembre 2024
In finance, matrices are essential for organizing and analyzing data like asset returns, correlations, and risks. They allow for compact manipulation of complex relationships, aiding in portfolio analysis, derivative pricing, and investment optimization.
A key matrix is the covariance matrix, Σ (Sigma), which captures how asset returns vary individually and with each other.