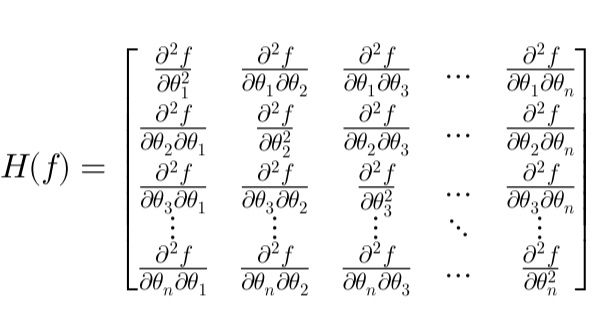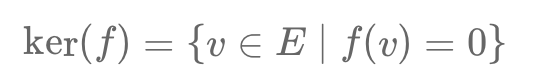Principes mathématiques et applications en finance · 05. mars 2025
La matrice hessienne, composée de dérivées partielles du second ordre, est un outil fondamental en optimisation financière et en valorisation des dérivés. Cet article simplifie son rôle dans l’identification des points critiques, les approximations quadratiques et la gestion des risques via le Gamma hedging.
Principes mathématiques et applications en finance · 20. décembre 2024
Le noyau est un concept clé en algèbre linéaire, représentant l’ensemble des vecteurs annulés par une transformation linéaire. Il joue un rôle essentiel en finance pour analyser les matrices de covariance, optimiser les portefeuilles et réduire la dimensionnalité des données. Utilisé dans la gestion des risques et l’optimisation financière, il identifie les redondances et simplifie les modèles tout en maintenant leur précision.
Principes mathématiques et applications en finance · 19. décembre 2024
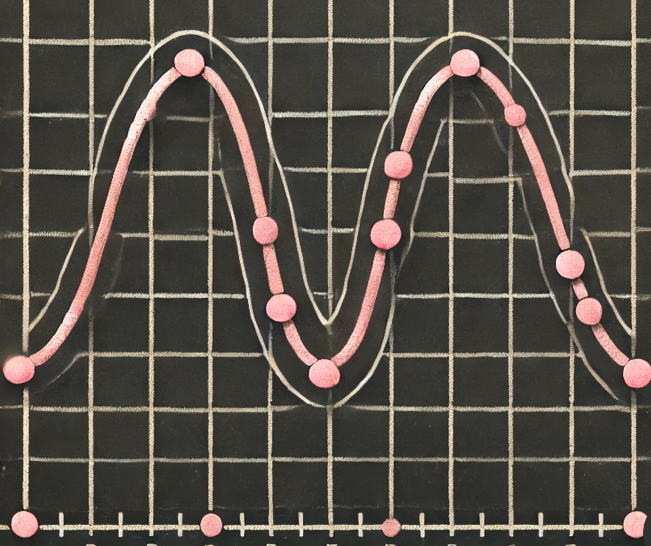
Le phénomène de Runge, identifié en 1901, survient lors de l’interpolation polynomiale avec des polynômes de degré élevé, provoquant des oscillations importantes, surtout aux extrémités de l’intervalle. En finance quantitative, cela impacte la construction de courbes de taux, les surfaces de volatilité implicite et la calibration de modèles, générant des artefacts non réalistes.
Mathematical Principles and Quantitative Finance · 01. octobre 2024
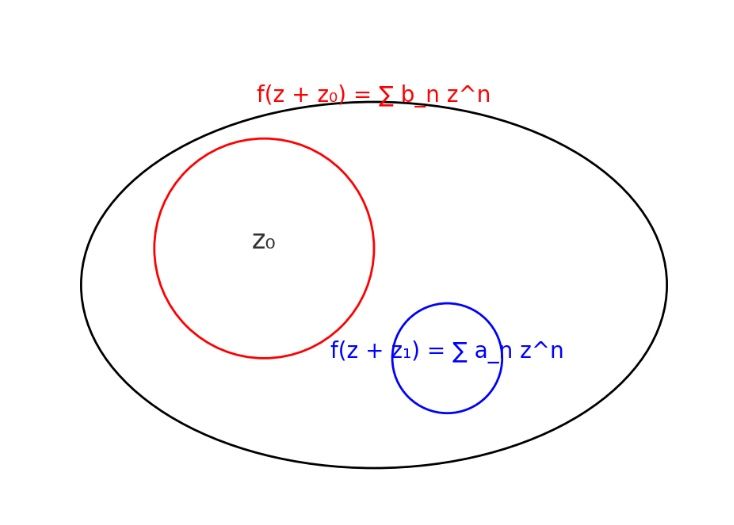
En finance quantitative, la valorisation des dérivés conditionnels, tels que les options, nécessite la convergence des fonctions de prix. Les ensembles compacts et fermés dans l’espace complexe assurent cette stabilité. Les fonctions analytiques dépendent de cette convergence pour une précision optimale, et la formule intégrale de Cauchy permet de calculer la valeur d'une fonction via une intégrale sur son contour.
Mathematical Principles and Quantitative Finance · 01. octobre 2024
Les fonctions indicatrices occupent une place fondamentale en mathématiques financières, car elles servent de conditions binaires pour l’évaluation des actifs risqués. Elles permettent d’agir comme des interrupteurs dans les formules, incluant ou excluant certains termes en fonction du respect de conditions précises. Par exemple, lors de l'évaluation de la valeur d'une obligation à coupon zéro dans un univers risque-neutre (*), nous tenons compte de la valeur actuelle attendue du...
Mathematical Principles and Quantitative Finance · 30. septembre 2024
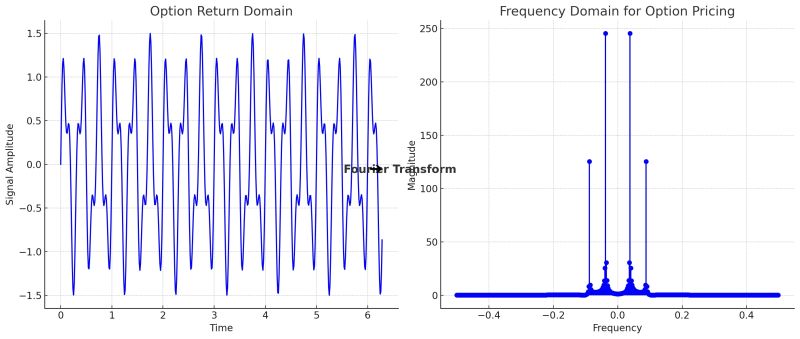
Option pricing, a key financial market challenge, relies on the Fourier transform to address complexities in valuation. An option grants the right to buy or sell an asset at a strike price, K, by expiration, T. The current price depends on the expected payoff, e.g., for a European call: max(S_T - K, 0). This is challenging as future asset prices follow complex stochastic processes.
The Fourier transform simplifies this by converting payoff calculations from time to frequency domain.