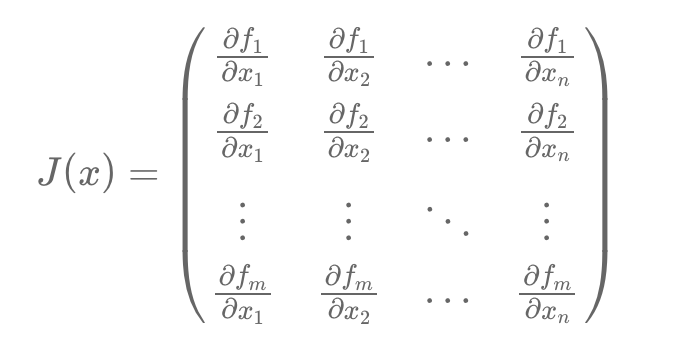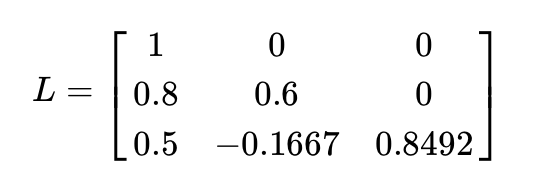Mathematical Principles and Quantitative Finance · 29. juin 2024
Cholesky decomposition plays a critical role in pricing Collateralized Debt Obligations (CDOs) by transforming independent variables into correlated ones based on a given correlation matrix. This method helps simulate scenarios of correlated defaults, essential for assessing risks and determining expected losses in CDO tranches.
Mathematical Principles and Quantitative Finance · 09. novembre 2023
In quant finance, eigenvalues and eigenvectors distill risk and trends in portfolio analysis. They're crucial in PCA, reducing complex asset return data to key risk factors. For instance, eigenvectors direct to axes showing variance, while eigenvalues quantify it, revealing how assets move together.
#EigenvaluesInFinance #EigenvectorsExplained #PrincipalComponentAnalysis #CovarianceMatrix
Mathematical Principles and Quantitative Finance · 24. septembre 2023
Unlock portfolio risk management with linear algebra & copula in layman’s terms. Master the art of pairs trading & optimize your asset allocation using easy steps. Dive into expected returns, covariance & portfolio weights. Mobile-friendly, updated insights! #FinanceEducation #RiskAnalysis
Mathematical Principles and Quantitative Finance · 25. mars 2023
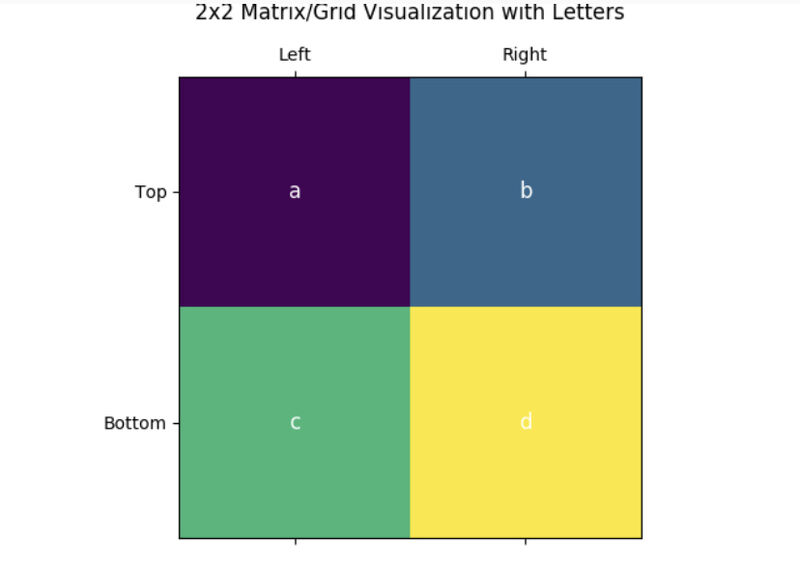
When trying to grasp the determinant of a matrix, envision a 2x2 grid, with values 'a' to 'd'. Picture it as arrows on a surface. The first column points as (a,c) and the second as (b,d). They form a slanted rectangle, a parallelogram. The formula 'ad - bc' signifies this shape's area. If negative, imagine viewing the shape from the opposite side. In essence, the determinant measures the space this shape occupies. Think of it as the "area" of the matrix's influence #MatrixDeterminant #MathBasic
Mathematical Principles and Quantitative Finance · 25. février 2023
Cholesky decomposition, in essence, breaks down complex financial data to simplify understanding of risk interplay between assets. Picture this as disassembling a LEGO house to discern how each block contributes to its stability. In finance, this "deconstruction" reveals correlations in asset portfolios. By identifying these foundational risk relationships, professionals can navigate market complexities more adeptly, akin to understanding the best LEGO block placements for a sturdy structure.