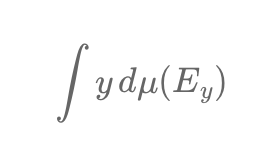Mathematical Principles and Quantitative Finance · 29. septembre 2024
Topology, from Greek "topos" (place) and "logos" (study), explores connections within spaces, focusing on structure over distance. In quantitative finance, topology is crucial for derivatives pricing, ensuring stable models and smooth price changes. It supports the convergence of models like binomial trees and Monte Carlo simulations, enhancing accuracy.
A key principle in finance is the absence of arbitrage – no risk-free profit.
Mathematical Principles and Quantitative Finance · 12. septembre 2023
The Lebesgue integral offers a powerful approach for tackling functions with numerous discontinuities, where traditional Riemann methods fail. This makes it invaluable in quantitative finance, enabling the modeling of sudden market jumps and refining risk management. Lebesgue-inspired techniques enhance financial models, capturing real-world market volatility.
Mathematical Principles and Quantitative Finance · 12. septembre 2023
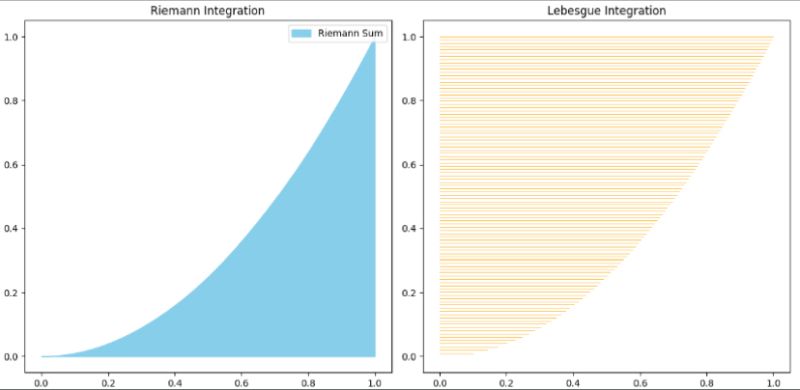
L'intégrale de Riemann divise l'axe (x) en intervalles pour calculer des aires de rectangles, mais échoue pour des fonctions "saccadées". L'intégrale de Lebesgue, en découpant l'axe (y), traite mieux ces discontinuités. Crucial en finance quantitative pour modéliser les sauts de prix et des risques extrêmes, offrant des modèles robustes comme le Jump Diffusion.