Mathematical Principles and Quantitative Finance · 12. septembre 2023

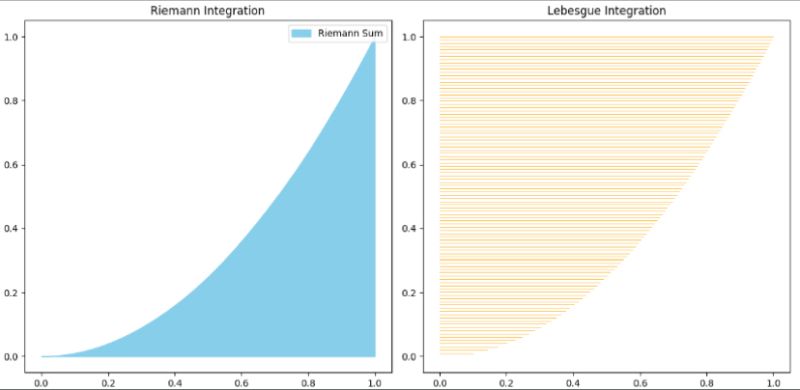
L'intégrale de Riemann divise l'axe (x) en intervalles pour calculer des aires de rectangles, mais échoue pour des fonctions "saccadées". L'intégrale de Lebesgue, en découpant l'axe (y), traite mieux ces discontinuités. Crucial en finance quantitative pour modéliser les sauts de prix et des risques extrêmes, offrant des modèles robustes comme le Jump Diffusion.