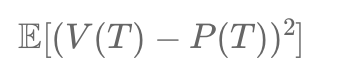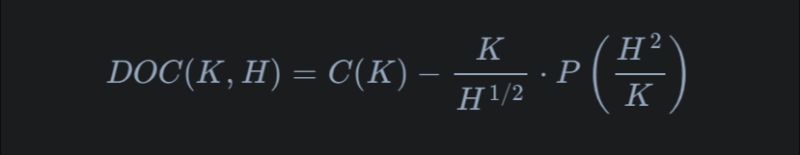Quant Interview Questions · 14. novembre 2023
Which of the following statements about Volga is most accurate? A. Volga is the rate at which vega changes with respect to the underlying price B. High Volga values imply that options are more sensitive to kurtosis risk of the underlying asset C. Volga becomes particularly important when trading binary options due to their vega profile D. All else being equal, an option with a longer time to maturity will always have a higher Volga than an option with a shorter time to maturity ------------- B....
11. novembre 2023
The Jump-to-Default Approach in option trading, modeled by an SDE, highlights how sudden stock price drops (J) affect low strike call options, especially under high credit risk. This contrasts with the Black-Scholes model, which assumes continuous price movements. In high-risk scenarios, the market often lowers the value of these options, factoring in potential defaults, and adjusts implied volatility accordingly. #OptionPricing #CreditRisk #FinancialMarkets #TradingStrategies #InvestmentRisk
Pricing et Valorisation d'instruments financiers · 11. novembre 2023
L'approche "Jump-to-Default" avec une EDS modélise la dynamique des prix des actions en intégrant les risques de défaut. Cruciale pour le trading d'options, elle explique pourquoi les options call deep in-the-money présentent une volatilité plus basse en contexte de risque de crédit élevé, par rapport au modèle Black-Scholes.
04. novembre 2023
Mean square hedging minimizes the gap between a hedging portfolio and an exotic option's payoff at maturity. It involves dynamic adjustments of holdings in risky and risk-free assets, guided by solving a stochastic differential equation and often requiring numerical methods like Monte Carlo simulations for implementation.
Stochastic Models and Processes · 08. septembre 2023
Unpack the myth that option Delta equals the probability of expiring in-the-money. Dive into risk-neutral valuation and the Black-Scholes model, where assets grow at a risk-free rate, making Delta an unreliable real-world probability indicator. Explore the distinction for smarter option trading. #OptionTrading #BlackScholes #RiskNeutralValuation
Mathematical Principles and Quantitative Finance · 19. août 2023
Explore the connection between Tesla's advanced speed regulator and the concept of gamma neutrality in options trading. While delta signifies the speed (akin to an option's price movement relative to its asset), gamma represents acceleration, indicating how delta evolves. Achieving gamma neutrality in trading parallels maintaining both speed and acceleration in a Tesla, ensuring a predictable and smooth drive.
15. juillet 2023
In simple terms, think of hedging like insurance. A bank sold a specific type of "insurance" (Down-and-Out European Call) that pays out only if the stock price doesn't dip below a certain level (the barrier). To safeguard itself, the bank uses a mix of buying and selling other financial "insurances" (call and put options). The magic formula ensures that if the stock dips below the barrier, the bank won't lose money. It's a balancing act, where buying one thing counteracts the selling of another
01. avril 2023
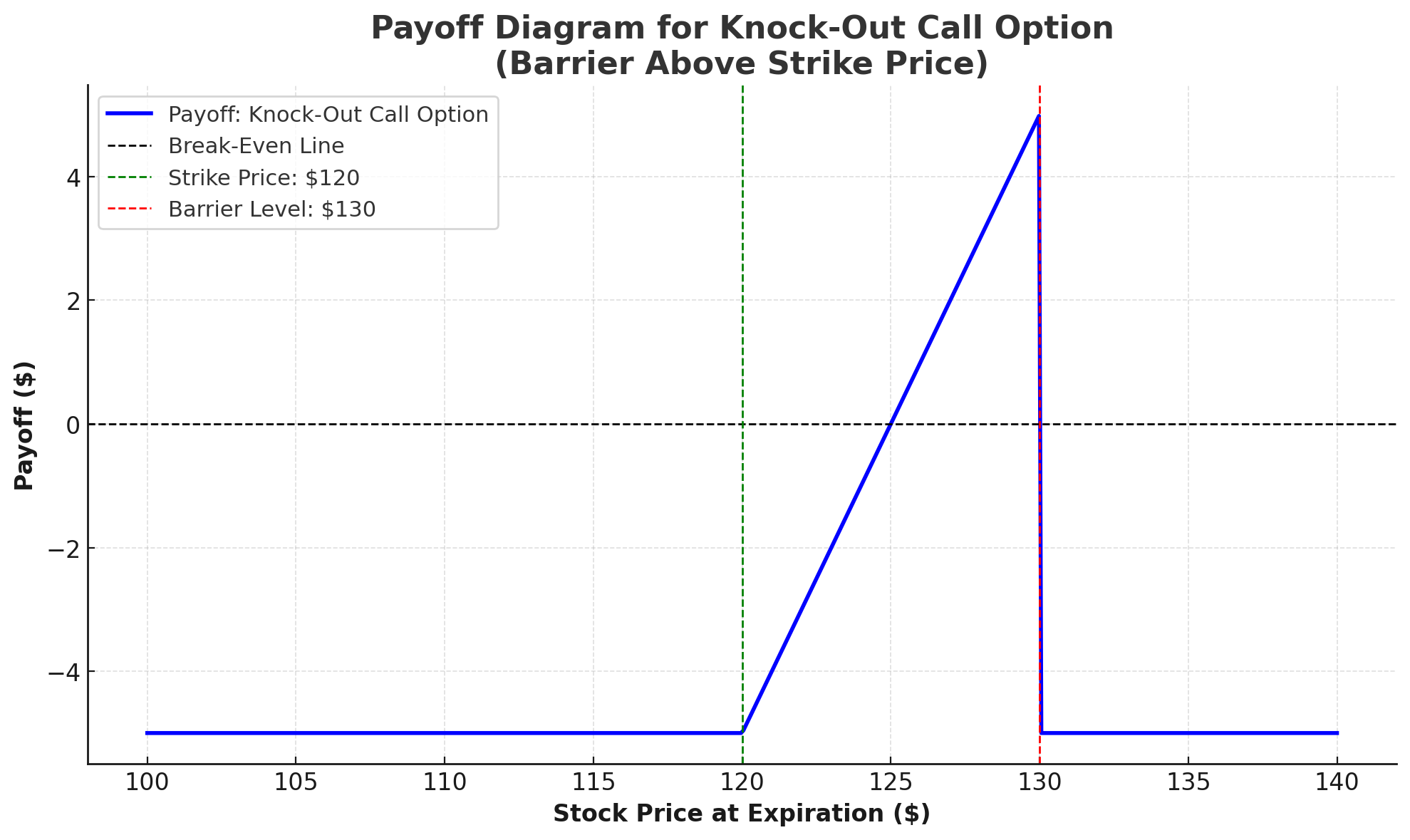
Bank sells a Knock-Out (KO) call option on Stock XYZ to a bullish trader. If stock hits $110, the option ends. To hedge risks like vega and vanna from the KO option, the bank uses a Risk Reversal (RR). They buy call options and sell put options on Stock XYZ. This manages volatility changes and price shifts, ensuring stable positions. If the stock reaches $110, the KO ends with no payout due. The RR helps the bank control risk.
#HedgingStrategies #RiskReversal #OptionsTrading #BarrierOptions