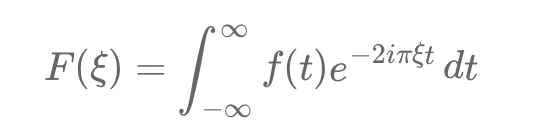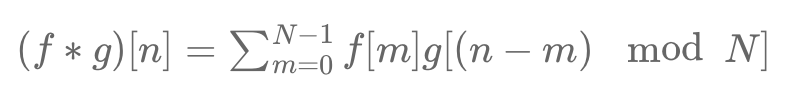Mathematical Principles and Quantitative Finance · 30. septembre 2024
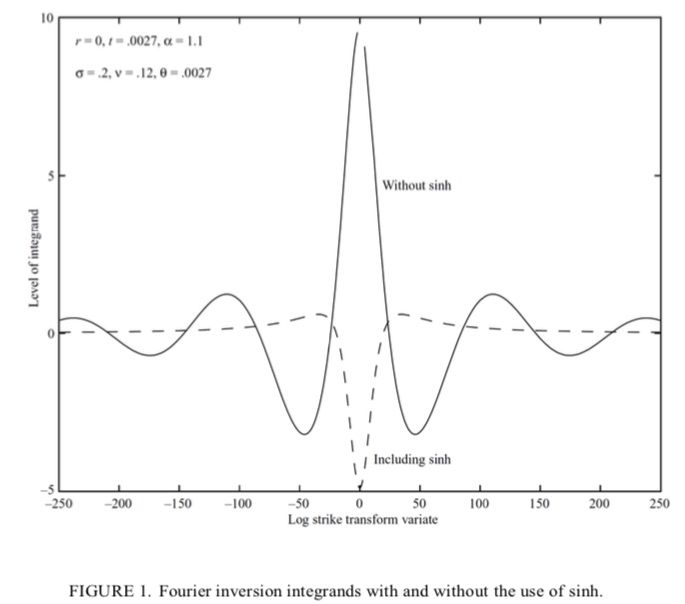
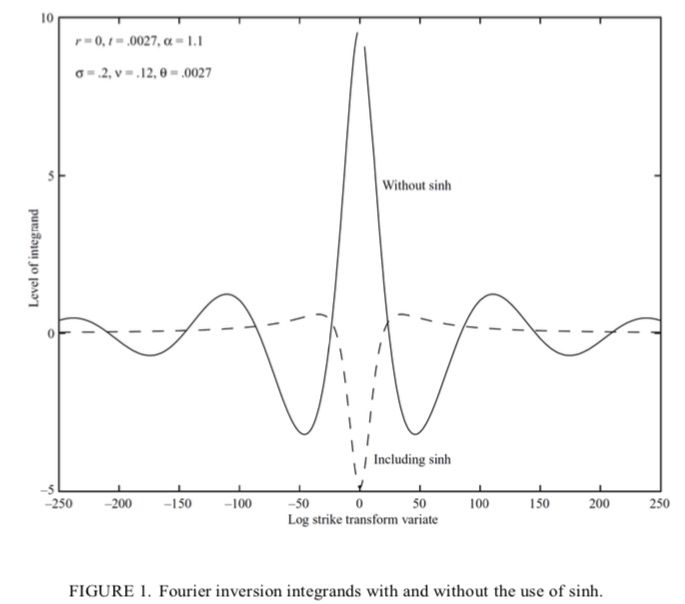
Option pricing, a key financial market challenge, relies on the Fourier transform to address complexities in valuation. An option grants the right to buy or sell an asset at a strike price, K, by expiration, T. The current price depends on the expected payoff, e.g., for a European call: max(S_T - K, 0). This is challenging as future asset prices follow complex stochastic processes.
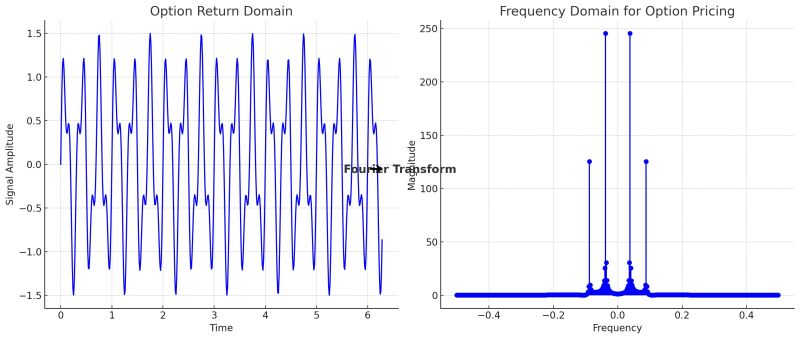
The Fourier transform simplifies this by converting payoff calculations from time to frequency domain.
Pricing and Valuing Financial Instruments · 30. septembre 2024
Option pricing, a key financial market challenge, relies on the Fourier transform to address complexities in valuation. An option grants the right to buy or sell an asset at a strike price, K, by expiration, T. The current price depends on the expected payoff, e.g., for a European call: max(S_T - K, 0). This is challenging as future asset prices follow complex stochastic processes.
The Fourier transform simplifies this by converting payoff calculations from time to frequency domain.
Mathematical Principles and Quantitative Finance · 19. avril 2024
The trigonometric circle extends complex numbers, useful for visualizing periodic phenomena. In option pricing, the binomial model reflects market uncertainty through a tree structure. Fourier transforms help analyze future payoffs, using the characteristic function of the underlying asset's distribution. Circular convolutions connect binomial models and Fourier transforms, facilitating efficient computation of option prices.