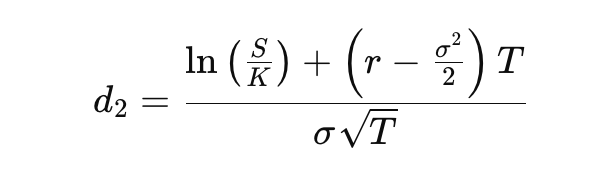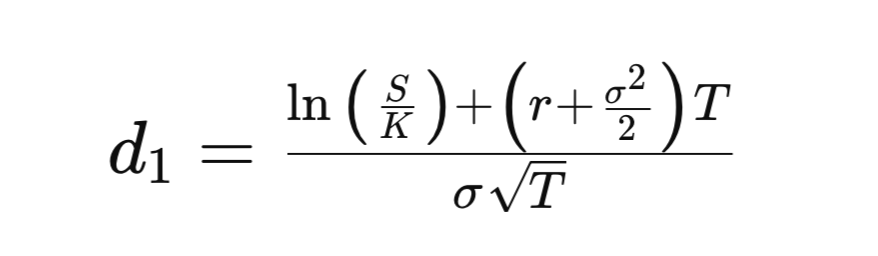Stochastic Models and Processes · 10. juin 2024
La formule de Black-Scholes pour une option d'achat calcule le prix de l'option en utilisant la probabilité d'exercer l'option, représentée par N(d2). Cette probabilité ajustée au risque assure une tarification sans arbitrage. Un N(d2) plus élevé signifie une probabilité accrue d'exercice de l'option, affectant le coût attendu et la valeur nette de l'option.
Processus et Modèles Stochastiques · 18. février 2023
Le terme d₁ dans la formule de Black-Scholes joue un rôle essentiel dans la tarification des options. Il englobe la position relative du prix de l’action par rapport au prix d’exercice, la valeur temporelle de l’argent et l'ajustement pour la volatilité. Cette formule capture l'ensemble des facteurs influençant la valeur d'une option.
Processus et Modèles Stochastiques · 11. février 2023
Découvrez une explication simple pour dériver l'équation de Black-Scholes. Que vous soyez étudiant en finance quantitative ou que vous cherchiez une remise à niveau, ce guide simplifié vous aide à comprendre cette PDE fondamentale étape par étape.