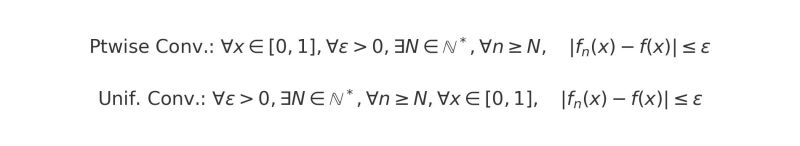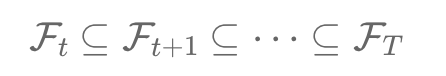Mathematical Principles and Quantitative Finance · 29. septembre 2024
Topology, from Greek "topos" (place) and "logos" (study), explores connections within spaces, focusing on structure over distance. In quantitative finance, topology is crucial for derivatives pricing, ensuring stable models and smooth price changes. It supports the convergence of models like binomial trees and Monte Carlo simulations, enhancing accuracy.
A key principle in finance is the absence of arbitrage – no risk-free profit.
Mathematical Principles and Quantitative Finance · 17. septembre 2024
Pointwise and uniform convergence are key mathematical concepts when working with sequences of functions, which are crucial in modeling financial assets. Pointwise convergence ensures that a sequence of functions converges to a target function at each individual point, ideal for analyzing specific market scenarios or prices. On the other hand, uniform convergence guarantees that the entire sequence converges at a uniform rate over an interval, which is essential for accurate valuation.
Mathematical Principles and Quantitative Finance · 30. avril 2024
The LASSO (Least Absolute Shrinkage and Selection Operator) method, developed by Robert Tibshirani in 1996, efficiently predicts outcomes while maintaining an accurate and minimalist model. In LASSO regression, the objective function minimizes the residual sum of squares (RSS) plus a penalty term involving a regularization parameter (λ) and coefficients (β_j) for predictors.
The penalty term encourages coefficient shrinkage towards zero, balancing data fit and model simplicity.
12. septembre 2023
Dive into the heart of finance with the sigma-algebra concept! Think of a deck of cards. Assigning probabilities, like drawing an Ace, means defining and combining events, and understanding their opposites. This structure, crucial in finance, ensures we consistently and meaningfully talk about events, especially in complex financial markets. As we track evolving information and model future possibilities, the sigma-algebra keeps our models from descending into chaos.