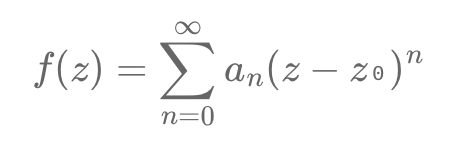Mathematical Principles and Quantitative Finance · 01. octobre 2024
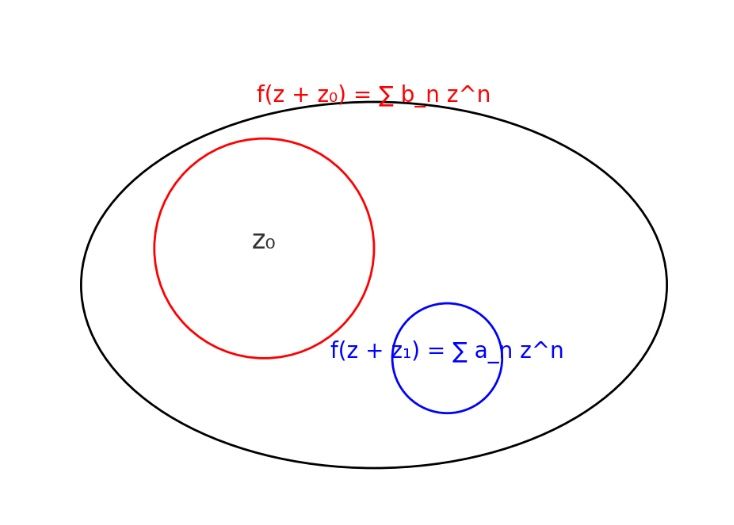
In quantitative finance, pricing conditional derivatives, like options, requires ensuring that price functions converge, meaning they stabilize as calculations are refined. Compact and closed sets in complex space help ensure this stability by keeping sequences bounded and finite. Analytic functions, which smoothly represent derivative prices, rely on this convergence for accuracy.
The Cauchy integral formula enables finding a function's value by integrating along a boundary contour.
Mathematical Principles and Quantitative Finance · 01. octobre 2024
En finance quantitative, la valorisation des dérivés conditionnels, tels que les options, nécessite la convergence des fonctions de prix. Les ensembles compacts et fermés dans l’espace complexe assurent cette stabilité. Les fonctions analytiques dépendent de cette convergence pour une précision optimale, et la formule intégrale de Cauchy permet de calculer la valeur d'une fonction via une intégrale sur son contour.