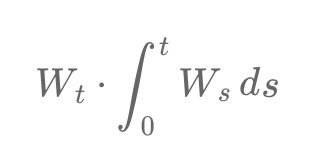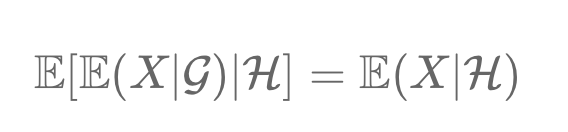Stochastic Models and Processes · 19. novembre 2023
Multiplying a Wiener process W_t by its integral creates a complex stochastic process, combining an instantaneous, "memoryless" state with its cumulative history. This nonlinear product, needing tools like Itô's lemma for analysis, reveals interactions between the current state and past values, crucial in financial mathematics for pricing path-dependent options.
Stochastic Models and Processes · 19. novembre 2023
The Tower Property in probability theory simplifies conditional expectations. It states that refining information from a broader σ-algebra (𝒢) to a narrower one (H) yields the same expectation as directly using H. In finance, it means mid-year portfolio predictions remain valid regardless of additional end-year information. This principle aids in effective portfolio management and risk assessment.
Stochastic Models and Processes · 21. octobre 2023
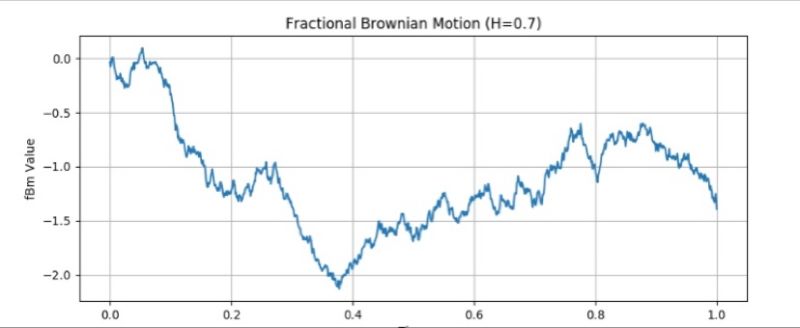
Fractional Brownian Motion (fBm) enriches classical Brownian motion by introducing the Hurst parameter (H), making it vital for modeling varying volatility in finance, physics, and beyond. With H dictating path roughness, fBm handles predictions in systems with long-range dependencies, aiding in asset volatility modeling and risk management. It's pivotal for understanding market behaviors and complex dynamics in diverse scientific fields.
Stochastic Models and Processes · 29. juillet 2023
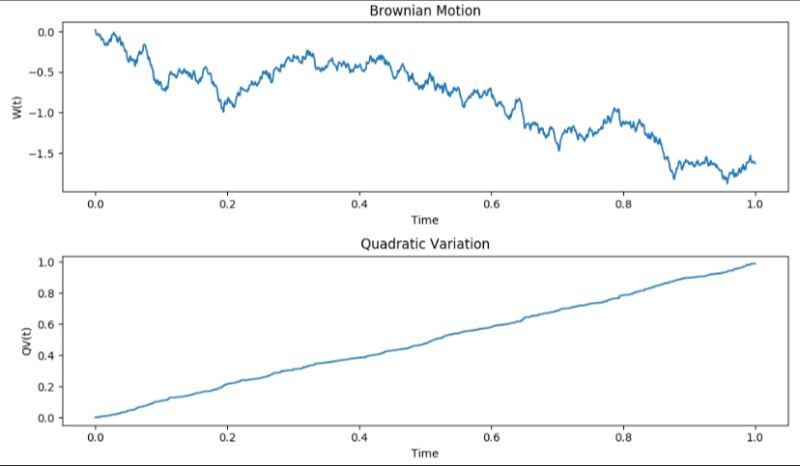
Explore the world of financial volatility with quadratic variation—a tool capturing asset "bumpiness". In finance, much like assessing a hiking trail's roughness, we gauge stock price fluctuations. With roots in Brownian motion, this metric offers insights into market behaviors, aiding predictions in high-frequency trading and refining the Black-Scholes model. Dive deep into market terrain with this crucial quantitative tool. #BrownianMotion #QuadraticVariation #QuantitativeFinance.