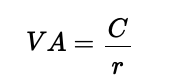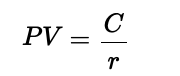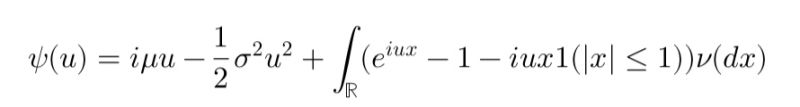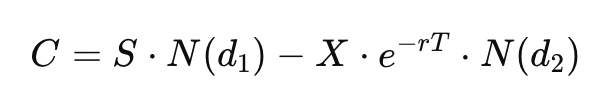Droit des marchés financiers · 02. avril 2025
Découvrez comment le droit évolue d’un système fondé sur la sanction vers une approche plus souple et adaptative. Cet article explore le rôle croissant du droit souple en droit financier, illustré par l’affaire LVMH – Hermès et l’intervention de l’AMF.
Principes mathématiques et applications en finance · 13. mars 2025
Une perpétuité est un instrument financier qui fournit des flux de trésorerie sans fin. Elle est utilisée pour évaluer des actions avec des dividendes fixes, l’immobilier avec des revenus stables, les obligations perpétuelles et la valorisation des entreprises. Lorsque les paiements augmentent au fil du temps, la valeur s’accroît, ce qui en fait un outil utile pour estimer des flux de trésorerie futurs en hausse.
Mathematical Principles and Quantitative Finance · 13. mars 2025
A perpetuity is a financial instrument that provides endless cash flows. It is used in valuing stocks with fixed dividends, real estate with stable income, perpetual bonds, and corporate valuation. When payments grow over time, the value increases, making it useful for estimating rising future cash flows. Based on geometric series, perpetuities are essential in finance for discounting long-term income streams.
Fonctionnement de Produits dérivés · 07. mars 2025
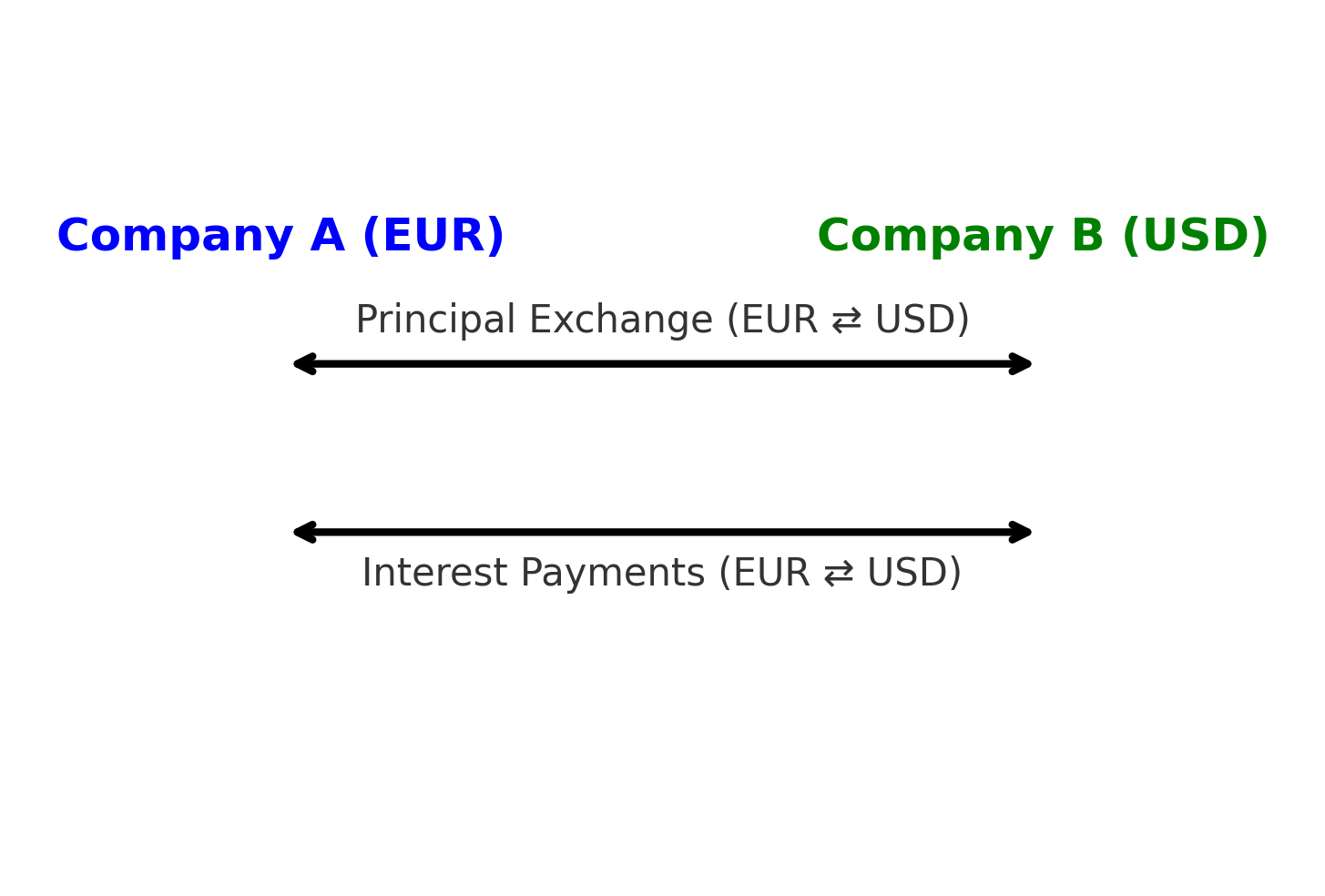
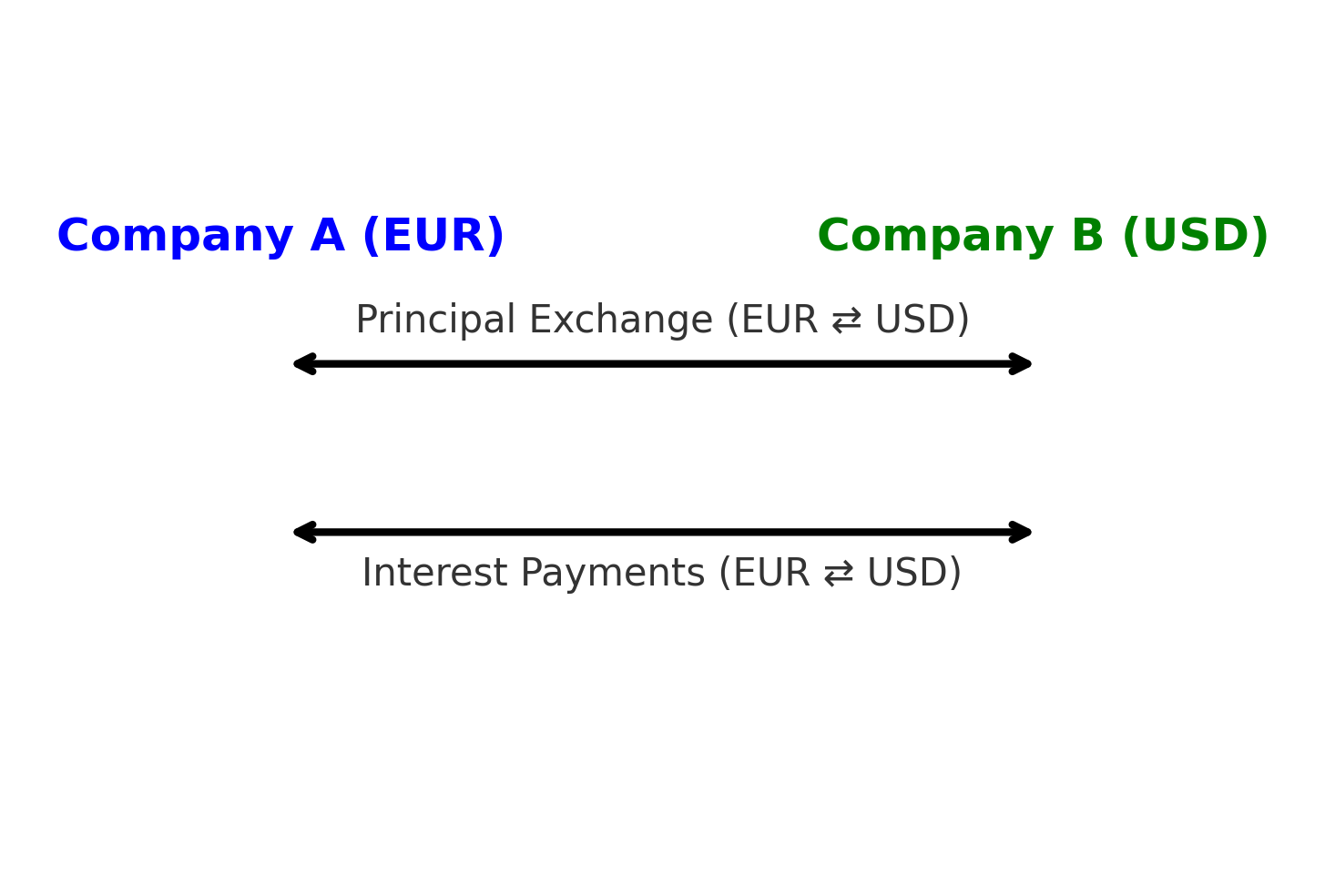
Les swaps de devises sont des accords financiers qui aident les entreprises à gérer les risques de change et à optimiser les coûts d’emprunt. Ces swaps permettent aux entreprises d’échanger des flux de paiement entre différentes devises tout en bénéficiant de taux d’intérêt plus avantageux.
Functioning of derivatives · 07. mars 2025
Currency swaps are financial agreements that help companies manage foreign exchange risks and optimize borrowing costs. These swaps allow businesses to exchange payment flows between different currencies while benefiting from more favorable interest rates.
Stochastic Models and Processes · 05. mars 2025
A Lévy process is a fundamental concept in probability theory and financial mathematics, extending Brownian motion by incorporating both continuous movements and discontinuous jumps. Characterized by independent and stationary increments, Lévy processes play a crucial role in modeling financial assets with sudden price changes, making them widely used in quantitative finance, risk management, and option pricing.
Fonctionnement de Produits dérivés · 05. mars 2025
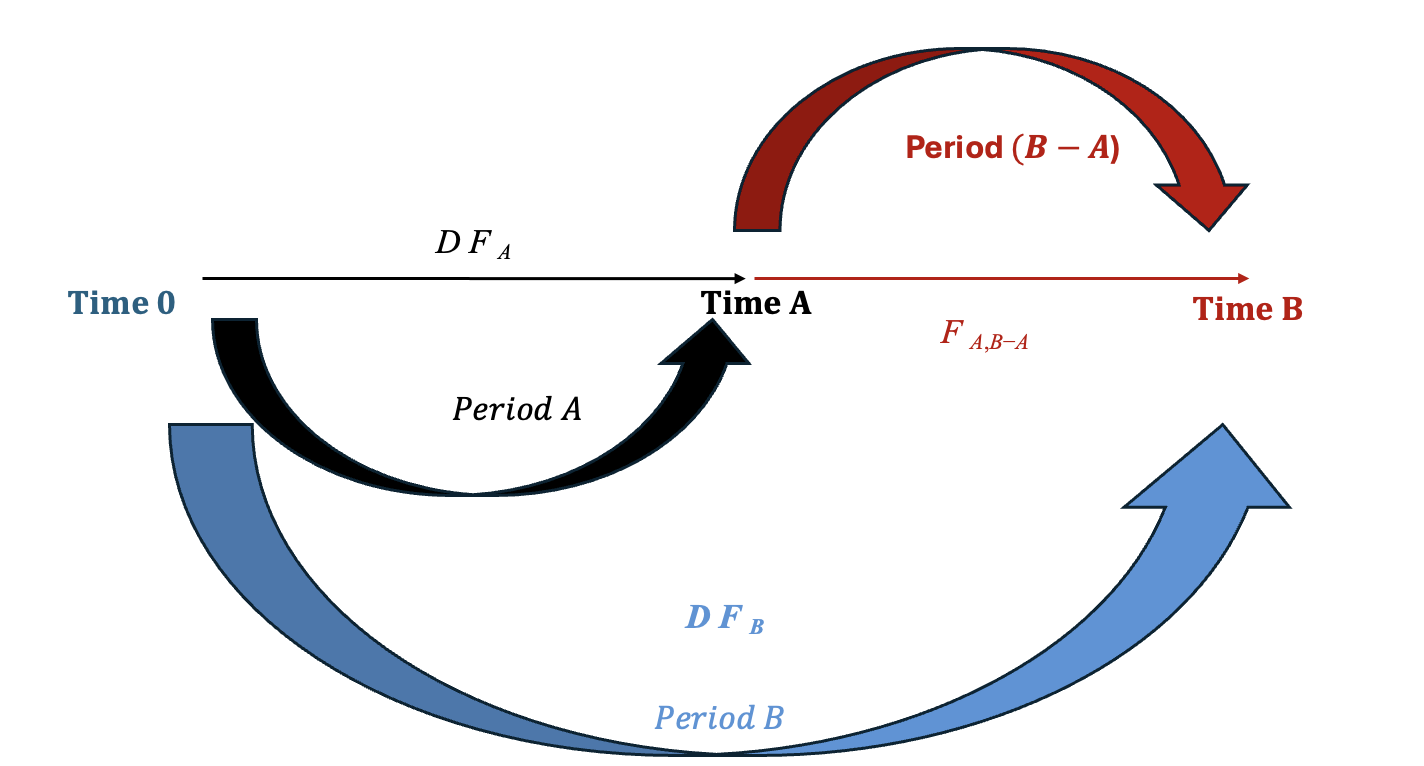
Le modèle de tarification à terme joue un rôle crucial sur les marchés à revenu fixe en garantissant que les investisseurs restent indifférents entre le fait de verrouiller un taux spot à long terme aujourd’hui ou de renouveler des investissements à court terme aux taux à terme. Ce mécanisme empêche les opportunités d’arbitrage, assurant ainsi l’efficacité du marché et une tarification équitable des obligations et des produits de taux d’intérêt.i
Processus et Modèles Stochastiques · 05. mars 2025
Dans le modèle de Black-Scholes, N(d1) et N(d2) agissent comme des indicateurs mesurant la probabilité de différents événements financiers. Imaginez un jeu où vous devez deviner si une action atteindra un certain prix. N(d1) représente votre meilleure estimation, en tenant compte des règles et des probabilités du jeu. De son côté, N(d2) indique combien vous devriez idéalement payer pour participer, en fonction de ces probabilités.
Processus et Modèles Stochastiques · 05. mars 2025
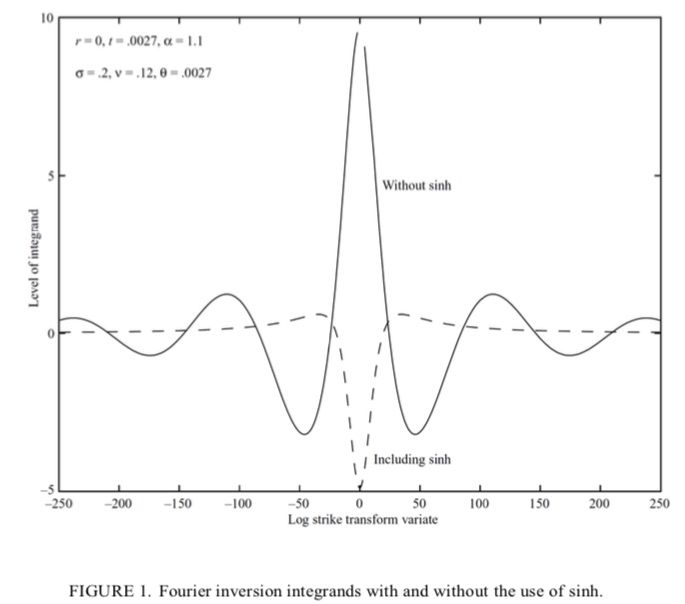
Découvrez comment la méthode de Carr & Madan exploite la transformée de Fourier pour la valorisation des options. Explorez les concepts clés, apprenez à atténuer les instabilités et améliorez les calculs numériques.