Laurent series extend Taylor series and have significant applications in quantitative finance for analyzing functions around singularities. They enable modeling asset prices, valuing options, and solving differential equations where singular behavior arises.
The Structure of Laurent and Taylor Series
A series is an infinite sum of terms expressed as \( a_0 + a_1 + a_2 + \dots \), which can either converge or diverge. For an analytic function, the Taylor series expansion around a point \( z_0 \) is given by:
\[ f(z) = a_0 + a_1 (z - z_0) + a_2 (z - z_0)^2 + \dots \]
where each coefficient \( a_n \) is related to the \( n \)-th derivative of the function evaluated at \( z_0 \). Taylor series are limited to regular (non-singular) regions of a function.
Laurent series generalize Taylor series by including terms with negative powers:
\[ f(z) = \dots + a_{-2} (z - z_0)^{-2} + a_{-1} (z - z_0)^{-1} + a_0 + a_1 (z - z_0) + \dots \]
These additional terms allow Laurent series to represent singularities, points where the function becomes infinite or undefined. The series thus separates a function into a singular part (negative powers) and a regular part (positive powers).
Regions of Convergence
For a Taylor series, the region of convergence is a disk centered at \( z_0 \), where the series represents the function within a radius \( R \):
\[ |z - z_0| < R. \]
Outside this radius, the series diverges, and the function can no longer be represented analytically by the Taylor expansion.
In contrast, the Laurent series has a region of convergence shaped like an annulus (or "crown") defined by two radii, \( R_1 \) and \( R_2 \):
\[ R_1 < |z - z_0| < R_2. \]
This annular region excludes \( z_0 \), making the Laurent series particularly useful for modeling singularities or poles.
Capturing Singularities
The Laurent series is essential for functions with singular behavior. For example, consider \( f(z) = \frac{1}{z - z_0} \), a function with a simple pole at \( z_0 \). The Laurent expansion for \( f(z) \) near \( z_0 \) is dominated by:
\[ f(z) = (z - z_0)^{-1}. \]
This term captures the singularity caused by the denominator approaching zero as \( z \to z_0 \). Higher-order negative powers, such as \( (z - z_0)^{-2} \), represent more complex singular behavior. These terms diverge as \( z \to z_0 \), accurately representing the behavior of the function.
Applications in Quantitative Finance
Laurent series are particularly valuable in finance, where market models often need to account for irregularities or extreme events, such as crashes or rapid changes in asset prices. For example:
- Modeling discontinuities in payoff functions for exotic derivatives.
- Representing singularities in complex pricing models, such as those involving stochastic volatility or jump diffusion processes.
- Solving differential equations that describe asset price dynamics, where singular points might represent thresholds or critical levels.
The Laurent series' ability to represent functions over an annulus allows for a richer analytic framework, especially when dealing with functions that are undefined or infinite at key points. This makes them indispensable in scenarios requiring precision modeling of singular behaviors.
Convergence Behavior
While the Taylor series converges within a disk, the Laurent series expands the region of convergence to a band-shaped annulus. This flexibility ensures that singularities, which are outside the scope of Taylor expansions, are effectively handled. By combining negative and positive powers, Laurent series provide a comprehensive tool for exploring complex function behaviors, particularly in scenarios involving poles or other singularities.

About the Author
Florian Campuzan, a graduate of Sciences Po Paris (Economic and Financial section) with a degree in Economics (money and finance), is a CFA charterholder and AMF-certified professional. He began his career in private equity and venture capital as an investment manager at Natixis before transitioning to market finance as a proprietary trader. In the early 2010s, he founded Finance Tutoring, specializing in market and corporate finance training and consulting.
For over 12 years, Florian has led finance training, advised financial institutions and industrial groups on managing risks, and prepared candidates for the CFA certification . Passionate about quantitative finance and the application of mathematics, he focuses on making complex concepts intuitive, believing that mastering any topic starts with understanding its core intuition.

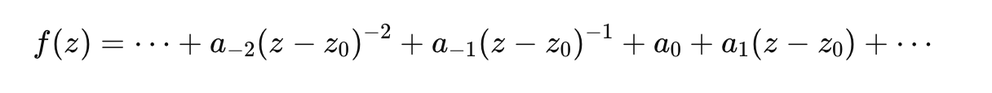
Écrire commentaire