La sous-additivité est un principe en gestion des risques qui suggère que la combinaison de deux ou plusieurs actifs risqués ne doit pas entraîner
un risque total supérieur à la somme des risques individuels. Ce concept repose sur l'idée que la diversification réduit généralement le risque. La formule de la sous-additivité peut être écrite comme suit :
ρ(A + B) ≤ ρ(A) + ρ(B)
où "ρ" représente la mesure du risque, et A et B représentent différents actifs ou portefeuilles. Si le risque total (ρ) du portefeuille combiné (A
+ B) est inférieur ou égal à la somme des risques des portefeuilles individuels (A et B), alors la mesure du risque est considérée comme sous-additive.
La sous-additivité est l'une des principales propriétés qu'une mesure de risque doit posséder pour être considérée comme une mesure de risque
cohérente.
La Valeur à Risque (VaR) est souvent critiquée pour ne pas toujours satisfaire la condition de sous-additivité.
La VaR est calculée comme un percentile spécifique de la distribution des pertes — par exemple, le 95e percentile. Cela signifie qu'elle mesure
uniquement la perte qui n'est pas dépassée avec un certain niveau de confiance (disons, 95 % du temps).
Cependant, elle ne fournit aucune information sur la taille potentielle ou la fréquence des pertes qui dépassent ce niveau. En d'autres termes, la
VaR ne nous dit rien sur la gravité des mauvaises issues au-delà de ce point, ce qui est souvent appelé le "risque de queue".
L'exemple suivant illustre le manque de sous-additivité de la VaR :
Imaginez 2 obligations dont la probabilité de défaut est de 4 % avec une valeur notionnelle de 10 millions de dollars et une perte en cas de défaut
de 100 % pour chaque obligation.
Avec un niveau de confiance de 95 %, la VaR pour chaque obligation individuellement serait de 0 $ car la probabilité de défaut (4 %) est inférieure
à notre seuil de VaR de 5 %. Cela signifie que nous sommes confiants à 95 % que la perte ne dépassera pas 0 $ en raison du défaut.
Pour trouver la probabilité qu'aucune obligation ne fasse défaut, nous multiplions la probabilité que chaque obligation ne fasse pas défaut.
Pour chaque obligation, c'est (1- 0.04), soit 96 %. Donc, pour les deux :
(1 - 0.04) * (1 - 0.04) = 0.9216
Pour trouver la probabilité qu'au moins une obligation fasse défaut, nous soustrayons la probabilité qu'aucune ne fasse défaut de 1
: 1 - 0.9216 = 0.0784 ou 7.84 %.
Étant donné que la probabilité qu'au moins une obligation fasse défaut (7.84 %) est supérieure à notre seuil de 5 %, nous devons considérer la
valeur notionnelle totale à risque. Ainsi, la VaR pour le portefeuille combiné est le montant notionnel total, soit 10 millions de dollars.
La CVaR (Conditional Value at Risk) pallie les lacunes de la VaR en fournissant une perte moyenne attendue dans les pires scénarios au-delà du seuil
de la VaR. Elle prend en compte la "forme" et la gravité du risque de queue, ce que la VaR ignore.
La CVaR est sous-additive, ce qui signifie qu'elle reflète correctement le bénéfice de la diversification.

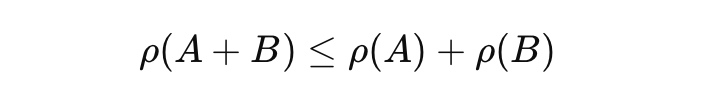
Write a comment