Une copule est un concept mathématique utilisé en statistiques pour décrire la relation entre plusieurs variables. Sa principale fonction est de capturer la structure de dépendance entre ces variables, indépendamment de leurs distributions individuelles.
Dans l'analyse multivariée, nous avons souvent affaire à plusieurs variables, chacune ayant sa propre distribution (marges). Une copule permet d'étudier et de modéliser comment ces variables sont liées (dépendance) indépendamment de leurs distributions individuelles.
Essentiellement, une copule prend les distributions individuelles des variables et les fusionne en une distribution multivariée conjointe. Cette distribution conjointe reflète non seulement les comportements individuels de chaque variable, mais aussi comment elles interagissent ou dépendent les unes des autres.
Les copules fonctionnent en utilisant les fonctions de répartition cumulatives (CDF) des variables, qui sont transformées en distributions uniformes sur l'intervalle [0, 1].
Après avoir transformé les marges en distributions uniformes, la copule modélise alors la structure de dépendance entre ces variables. Elle « lie » essentiellement ensemble les distributions uniformes séparées, créant une distribution multivariée qui reflète les dépendances.
La copule de Gumbel est un membre de la famille des copules archimédiennes. Elle est particulièrement bien adaptée pour modéliser les dépendances de queue, en particulier pour les variables qui ont tendance à montrer des valeurs extrêmes simultanément.
La copule de Gumbel C(u, v) est définie à l'aide de la formule : C(u, v) = exp(-[ (-log u)^θ + (-log v)^θ ]^(1/θ)) où u et v sont les fonctions de répartition cumulatives (CDF) des variables, et θ est un paramètre qui contrôle la force de la dépendance, avec θ ≥ 1.
Des valeurs plus élevées de θ indiquent une dépendance de queue plus forte.
Considérez deux actifs financiers, A et B, qui font partie d'un CDO. Nous sommes intéressés à comprendre le risque de défauts conjoints.
Supposons que nous ayons des données historiques de défaut pour ces actifs. Disons que les probabilités de défaut (dans un an) pour les actifs A et B sont respectivement de 5 % et 10 %.
Pour cet exemple, nous choisirons une valeur de θ supérieure à 1 pour refléter la dépendance, disons θ = 2. Cela indique une dépendance plus forte, en particulier dans les queues.
D'abord, nous transformons les probabilités de défaut en distributions uniformes. Pour simplifier, utilisons directement les probabilités de défaut comme nos valeurs uniformes. Donc, u (pour l'actif A) = 0,05, et v (pour l'actif B) = 0,10.
En insérant les valeurs :
u = 0,05, v = 0,10, et θ = 2.
Nous calculons (-log(0,05))^2, (-log(0,10))^2, puis ajoutons ces valeurs.
Élevons la somme à la puissance de 1/2 (puisque θ = 2), et appliquons finalement la fonction exponentielle.
La probabilité conjointe que les deux actifs A et B fassent défaut simultanément dans l'année, sous nos hypothèses, est d'environ 2,29 %.
Dans le contexte du pricing des CDO en 2008, l'utilisation d'un tel modèle qui met l'accent sur les dépendances de queue (comme la copule de Gumbel) aurait pu fournir une évaluation plus réaliste du risque par rapport aux copules gaussiennes.
#GumbelCopula
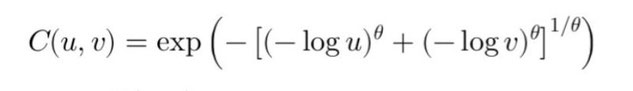
Écrire commentaire